Single-Speaker End-to-End Neural Text-to-Speech Synthesis
Thu 13 December 2018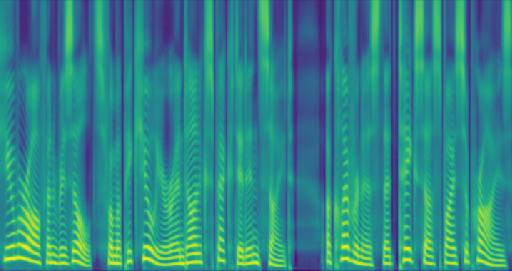
Figure 1: Example of a raw linear scale magnitude spectrogram generated by the post-processing component.
Abstract
Producing speech is a natural process for humans, but challenging for computers. Text-to-Speech (TTS) synthesis is generally considered a large scale inverse problem, transforming short written sentences into waveforms. This transformation is highly ambiguous and is influenced by many factors that are difficult to model. Traditional systems are based on complex multi-stage hand-engineered pipelines, requiring extensive domain knowledge; posing a significant challenge to model. This thesis introduces and analyzes a neural end-to-end generative speech synthesis architecture derived from Tacotron [1]. Instead of having humans identify and extract complicated rules and patterns, the computer learns to produce speech from unaligned text-audio-pairs. All components are described and training behavior as well as component effects are analyzed. Using a paired comparison 5-scale Mean Opinion Score (MOS) test comparing the proposed system against two current TTS reference systems it achieves a score of 3.4.
Download
| Source | Description |
|---|---|
| Master Thesis (PDF) | Master thesis describing this approach in detail. |
| yweweler/single-speaker-tts | Implementation of the described architecture using TensorFlow. |
Architecture
The proposed system directly derives from the Tacotron architecture [1]. Like Tacotron it employs a seq2seq encoder-decoder architecture with attention integrated into the decoder. A schematic of the architecture is illustrated in figure 2.
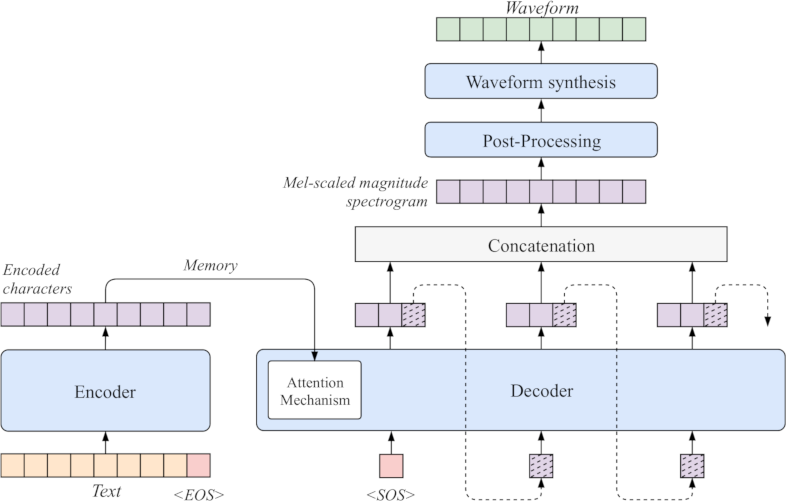
Figure 2: Schematic diagram of the proposed model architecture. It receives text as input and models speech as a waveform. The encoder produces a fixed size embedding for each character in the text.
The model receives a written sentence in the form of text as input and models speech in the form of a waveform. The architecture is divided into four consecutive stages. The encoder processes the written text and produces a fixed-size embedding for each character. By iteratively producing spectrogram frames the decoder stage generates a mel scale magnitude spectrogram (MSMSPEC) from this fixed-size embedding. The subsequent post-processing stage is used to clean and refine the spectrogram. It also transforms the mel spectrogram into a linear scale magnitude spectrogram (LSMSPEC) for the final waveform synthesis.
Model Components
This section gives an overview over the fundamental components needed for construction of the model.
CBHG Module
A 1-D convolution bank + highway network + bidirectional GRU (CBHG) module is a combination of multiple NNs, designed with the purpose of extracting representations from sequences [1]. A schematic overview of a CBHG module can be seen in figure 3.
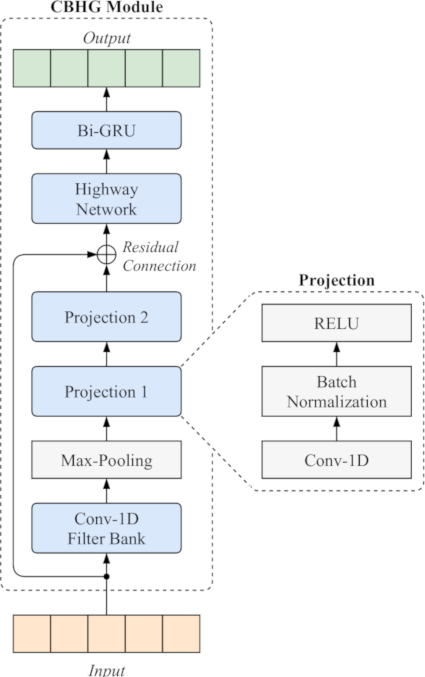
Figure 3: Schematic diagram of a CBHG module. The input sequence is first processed by a 1-D convolutional filter bank. Extracting representations comparable to N-grams. These are further compressed down to the dimensionality of the input sequence using two projections. The output of these projections is added to the modules input using a residual connection. Finally, a multi-layer highway network and a bidirectional GRU produce the output sequence.
Attention Mechanism
The proposed model utilizes a seq2seq architecture. In the past such approaches commonly compressed all information into a fixed-dimensional vector. However, the fixed-size compression leads to restrictions as the sequence lengths increase. Here the attention mechanism comes into play to eliminate the restrictions. Rather than presenting a fixed representation of a variable length sequence to the decoder, it is presented all information; selecting only the relevant data as needed.
Note that Instead of Bahdanau attention [2] as proposed by Tacotron [1] this work implements Luong attention [3]. Specifically the global approach using the dot product scoring function.
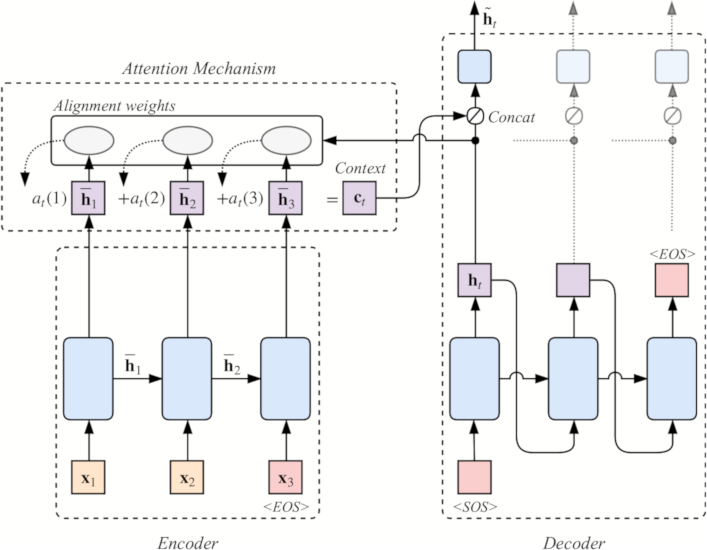
Figure 4: Global Luong attention mechanism using GRU RNN cells. At each decoder time step \(t\) the model infers a variable-length alignment weight vector \(a_{t}\). This vector is based on the current target state \(h_{t}\) and all source states \(\overline{h}_{s}\). Afterwards a global context vector \(c_{t}\) is computed as the weighted average of encoder source states using the alignment weights \(a_{t}\).
Encoder
The encoder is the first processing stage in the architecture. Its main purpose is to generate a robust sequential representation of the text it receives as input. A schematic overview of the encoder can be seen in figure 6.
First for each character of the entered sequence a fixed-size character embedding is generated. Additionally, the virtual end of sequence (EOS) and the padding (PAD) symbols are assigned an embedding as well. The EOS symbol is appended to each written sentence such that the encoder’s RNN has a clear indication to when a sentence ends. The convolutional filter banks used in the CBHG module explicitly model local and contextual information comparable to modeling unigrams, bigrams, up to N-grams for text [1]. Since the CBHG module incorporates a bidirectional RNN it additionally provides sequential features both from the forward and the backward context. Note that the output still contains the same number of elements (although higher dimensional) as the encoder input has characters.
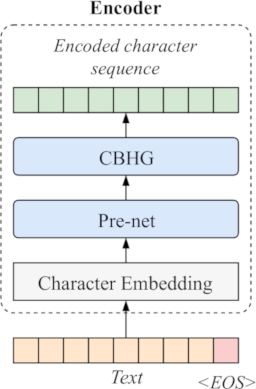
Figure 6: Schematic diagram of the encoder stage. The entered text is transformed into character embeddings of higher dimensionality. These embeddings are passed through a pre-net and a CBHG module to extract a robust high-dimensional representation for each character of the text.
Decoder
The decoder is the central component of the model. Based on the encoded characters it receives from the encoder it generates a MSMSPEC that is suitable for later synthesis. See figure 7 for a schematic of the decoder.
The decoder does not generate the MSMSPEC target in a single step, but rather models it as a sequence of spectrogram frames. With each decoding iteration a set of \(r\) individual non-overlapping frames is produced. Since the decoder is an attention based seq2seq decoder there is no direct connection between the encoder’s output and the decoder RNN cell input. The actual input for to each iteration is a single spectrogram frame. The encoded text representation from the previous stage is fed as the “memory” to an attention mechanism. This data flow can be seen in figure 2.
The process of generating \(r\) subsequent non-overlapping frames at each decoder step is an important design choice. When predicting \(r\) frames in one decoder step, the total number of decoder steps required divides by \(r\). This in turn reduces the training and inference times while also reducing the model size. This trick substantially increases convergence speed, as measured by a much faster and more stable alignment learned from attention. [1]
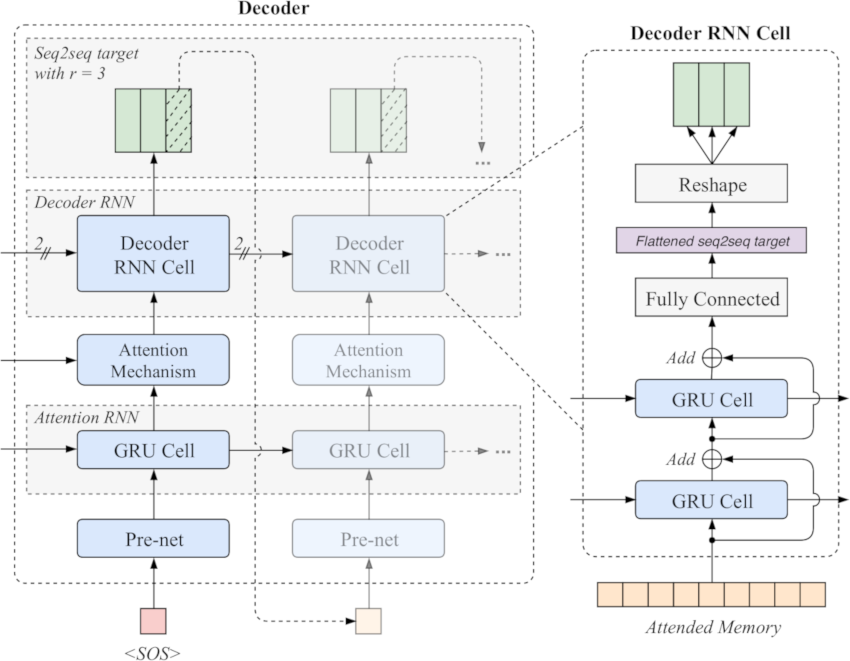
Figure 7: Schematic diagram of the decoder stage. Single MSMSPEC frames are fed as input to produce a set of \(r\) subsequent non-overlapping spectrogram frames at each decoding step. Starting with a start of sequence (SOS) frame each input first passes a pre-net and an attention RNN producing a robust sequential input for the attention mechanism. The attention mechanism uses it to derive new alignment weights and select encoder character representations for the current decoding step. It produces the “attended memory” which is then decoded into the sequence of \(r\) spectrogram frames using a stacked residual GRU RNN. The last of the \(r\) frames is then fed as input to the next decoder step.
Post-Processing
The post-processing stage is the last neural network based stage of the model. A schematic of this stage is shown in figure 8. Post-processing has two main tasks. First it enhances the MSMSPEC it receives as input by correcting decoder prediction errors. Second it converts the input into a LSMSPEC suitable for waveform synthesis.
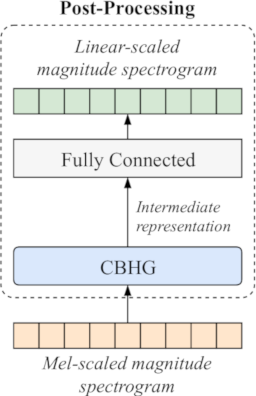
Figure 8: Schematic of the post-processing stage. A CBHG module reduces artifacts and errors in the MSMSPEC producing an intermediate representation. This representation is transformed into a LSMSPEC using a fully connected layer. The intermediate representation is not expected to be a spectrogram.
Waveform Synthesis
Waveform synthesis is the final stage of the architecture. Like in [1] it uses the Griffin-Lim algorithm to synthesize a waveform signal from the LSMSPEC the post-processing stage produces. The algorithm iteratively minimizes the Mean Squared Error (MSE) between the STFT of the reconstructed signal and the target signals STFT.
As hinted by Wang et al., while Griffin-Lim is differentiable, it does not have trainable weights [1]. Hence, it is not a neural component and therefore it is not optimized through training. Prior to feeding the predicted magnitudes to the algorithm, they are raised by a power of 1.3 as it is reported to reduce artifacts in the reconstructed signal [1].
Results
| Audio | Sentence |
|---|---|
| The garden was used to produce produce. | |
| The insurance was invalid for the invalid. | |
| The birch canoe slid on the smooth planks. | |
| Can you can a can as a canner can can a can? | |
| The weather was beginning to affect his affect. | |
| I had to subject the subject to a series of tests. | |
| How much wood would a woodchuck chuck if a woodchuck could chuck wood? | |
| Peter Piper picked a peck of pickled peppers. How many pickled peppers did Peter Piper pick? |
Alignments
An illustration of the produced attention alignments from a model trained on the Blizzard dataset can be seen in figure 9.
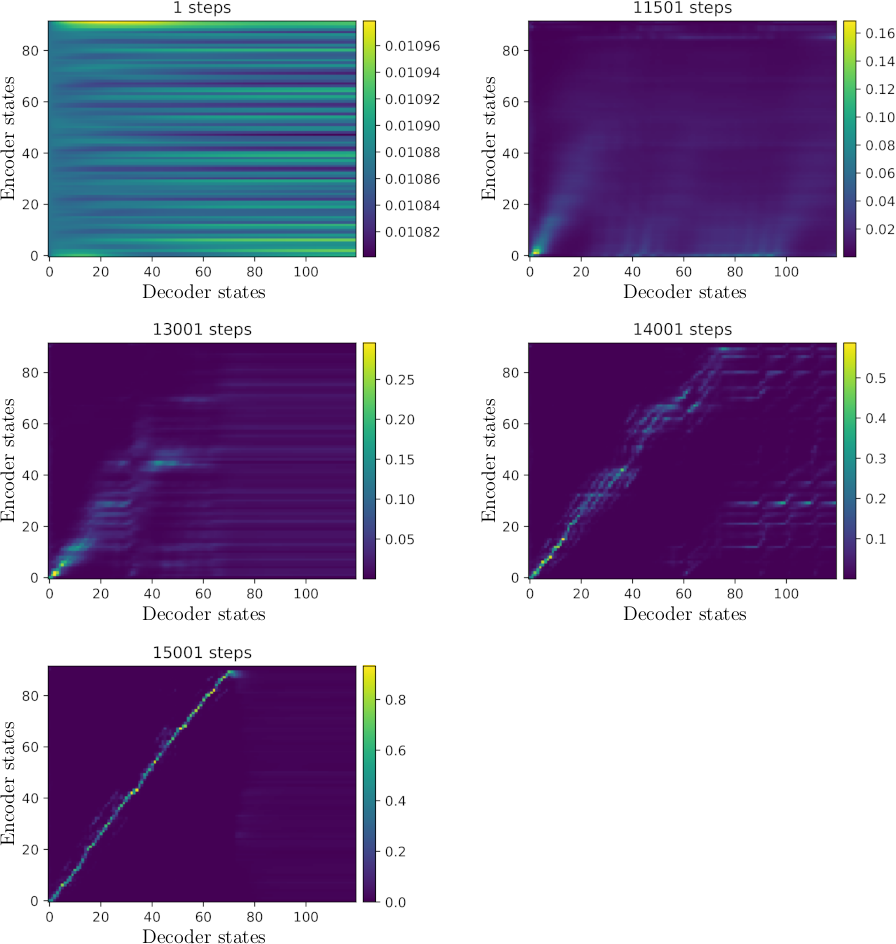
Figure 9: Progression of the attention alignment during inference at different stages of model training. Each encoder state corresponds to a character of the input sentence. Each decoder state corresponds to t spectrogram frames. All alignments are generated for the same randomly chosen utterance from the test portion of the Blizzard dataset. Note that the alignments in each column sum up to 1.
Feature Sizes
To assess the impact of the number of mel filter banks multiple models with 20, 40, 80, 120, 160 banks are compared All the models are trained for 200.000 iterations on the same train and test portions of the LJ Speech v1.1 dataset.
figure 10 shows the influence of the number of mel banks on the decoder loss during training. figure 11 illustrates the influence on the post-processing loss. The effect of the number of banks on the total evaluation loss can be seen in figure 12.
Increasing the number of banks lead to an increase in total loss during training, while reducing the number of banks reduces the total loss. As can be seen in figure 10 while the decoder loss reduces, the post-processing loss shown in figure 11 remains overall consistent. The uniform evaluation losses from figure 12 confirm that the post-processing loss remains consistent. This implies, that predicting the post-processing target does not suffer from the reduced decoder target size. But it also indicates, that the architecture has difficulties predicting a decoder target with increasing size. Hence, either the number of parameters in the decoder RNN cell has to increase to better capture the increased decoder target. Or another way of transforming mel into linear scale spectrograms has to be devised to reduce the post-processing loss.
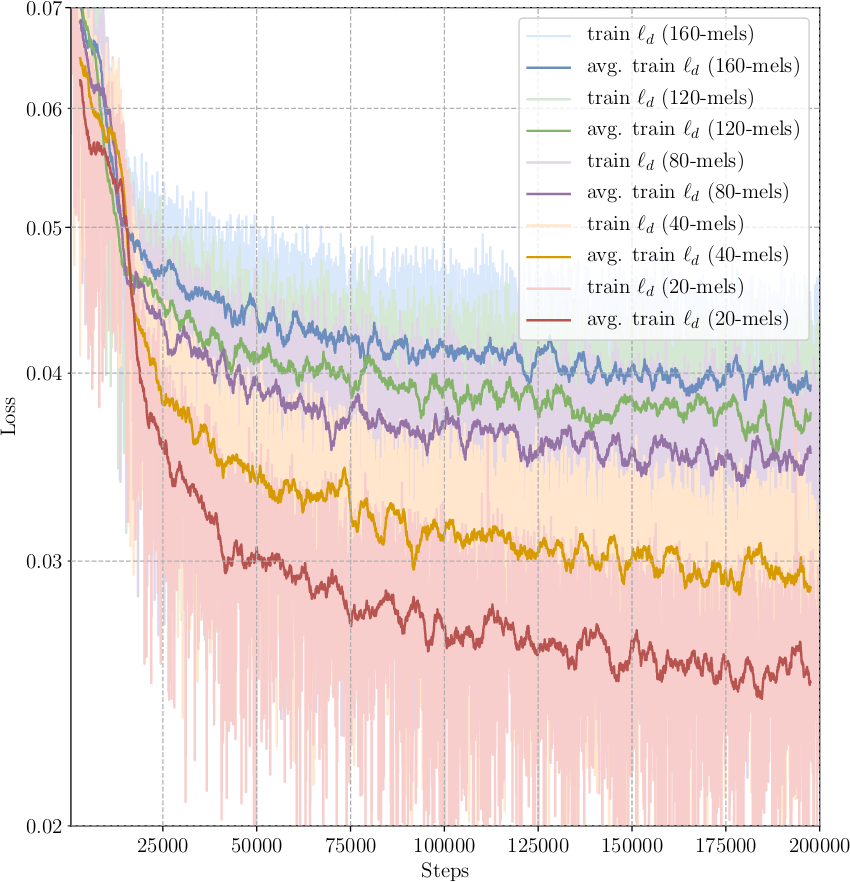
Figure 10: Progression of the post-processing loss during training for models using different amounts of mel banks as the decoder target. All models are trained on the Blizzard dataset and the losses are plotted every 50 steps. A moving average is calculated for all training plots using a window width of 50 and a stride of 1. The average is only calculated when the window completely overlaps with the signal. For better scaling the first 1,000 steps are omitted.
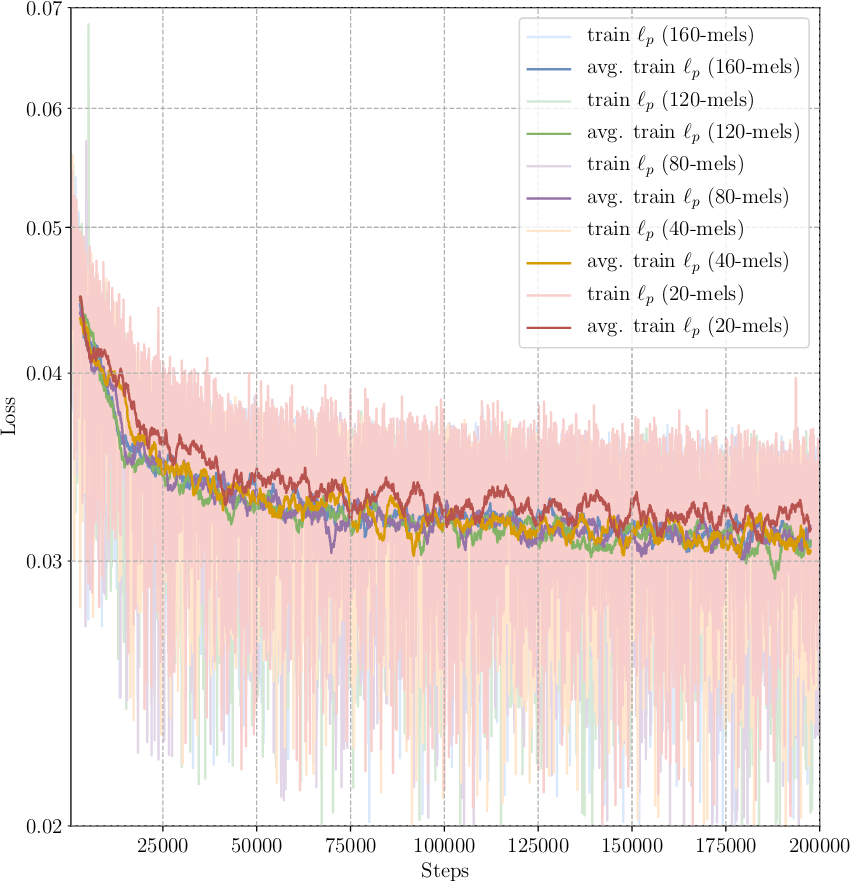
Figure 11: Progression of the post-processing loss during training for models using different amounts of mel banks as the decoder target. All models are trained on the Blizzard dataset and the losses are plotted every 50 steps. A moving average is calculated for all training plots using a window width of 50 and a stride of 1. The average is only calculated when the window completely overlaps with the signal. For better scaling the first 1,000 steps are omitted.
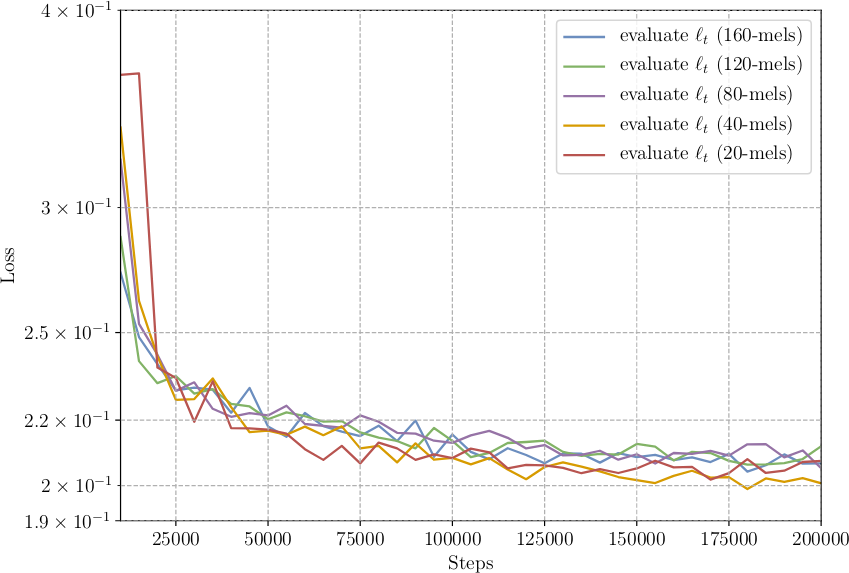
Figure 12: Progression of the total evaluation loss for models using different amounts of mel banks as the decoder target. The losses are plotted every 5,000 steps. The first 10,000 steps are skipped for better scaling.
